シールの密封理論について

なぜシールが漏れを止めることが出来るかの理論を説明いたします。
ただ、理論となれば、難しいと思われるかもしれませんが、このシール概論ではそのような展開はしません。
あくまで、シールは漏れを止めるかを最初にＯリングから話に入り、少し最近の文献や本からを参考にしながら、説明をしたいと思っています。

 

Ｏリングの密封理論

何時も、説明していますように、Ｏリングがハウジング内でつぶしを与えることにより、接触圧力または応力（反発力）が発生します。（前回までのFEMでも紹介したとおりです）
下図はその状態を示しています。

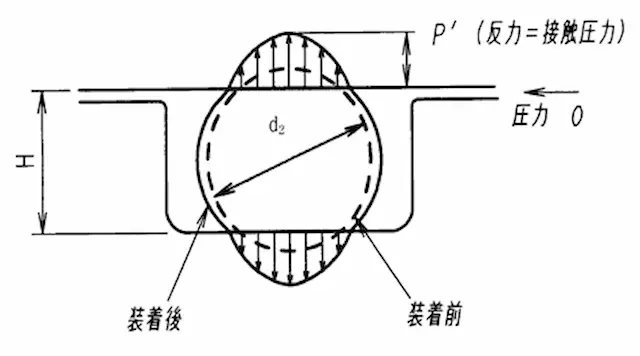
Ｏリングの密封機構

 

太さ（線径）d₂が溝深さHで圧縮されています。
これがつぶし代を与えることになります。
つぶし代(mm)=
(d₂-H)d₂
×100(％)　です。

当然、接触圧力を上げる手段には、つぶし代を増加する（溝深さを浅く）か、ゴムの硬さを上げることで出来ます。
図のように右側から圧力のない流体が来た場合には、この接触圧力(P´)が壁となり、漏れないことになります。
次に圧力が掛かった場合の図は次のとおりです。

 

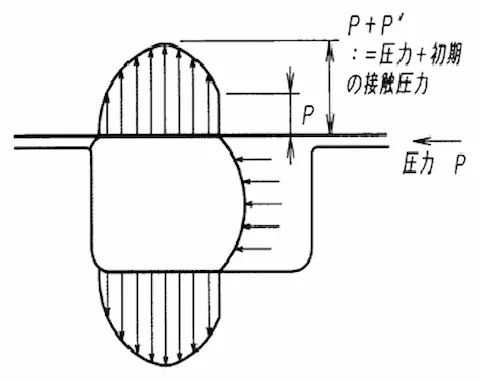
先ほどと異なるのは、接触圧力に掛かる圧力が加わる点です。従って、加圧された流体は漏れないことになります。
このことをシールの自封性と言います。
Ｏリング以外でのシール類（Ｕパッキン、Ｘリング、Ｔリング、組合せシール）も大半はこのような自封性を用いています。

この自封性を理論で説いたものがありますので、紹介します。文献は以前説明しましたFluid Sealing Technology Hydraulic Seals (著者：Heinz K Müller)を使用します。

 

シールの自封性の理論

角リングでの場合で説明いたします。

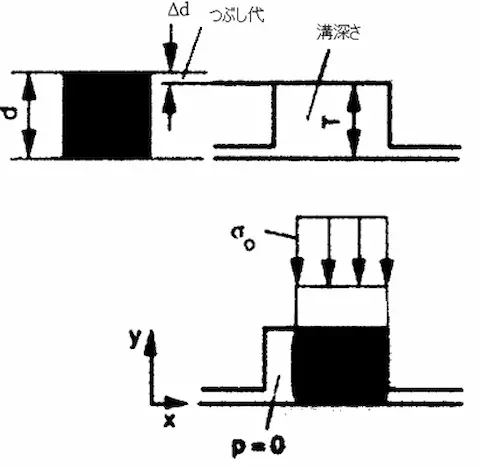
図2.1　角リングの接触圧力図

 

角リングの接触圧力はＯリングと異なり、同じ高さとなります。

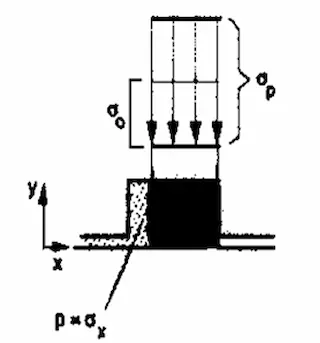
図2.2角リングの加圧時の接触圧力図

 

この上図は前号のＯリングと同じ形態となっています。（加圧により応力は増加）

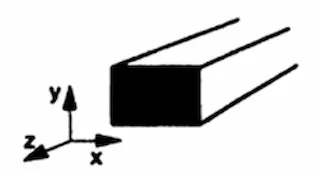
図2.3　角リングの3次元方向図

 

E・ε_x=σ_x－v・(σ_y+σ_z)…(1)
E・ε_y=σ_y－v・(σ_z+σ_x)…(2)
E・ε_z=σ_z－v・(σ_y+σ_y)…(3)
v：ポアソン比、E：ヤング率、ε：ひずみ、σ：応力です。
P=σ_x=0(図2.1から)
また、⊿d=d－T
ε_y=ε₀=
⊿dd
　となります。
式(2)(3)に代入すると
E・ε₀=σ₀－v・σ_z
0=σ_z－v・σ₀
従って
E・ε₀=σ₀・(1－v²)
または
σ₀=E・ε₀/(1－v²)…(4)
流体圧力が加わった場合、(2)(3)式から
E・ε₀=σ_p－v・(σ_z+P)…(5)
0=σ_z－v・(P+σ_p)
σ_z=v・(P+σ_p)…(6)
(4)(6)から
σ₀(1－v²)=σ_p－v・{v・(P+σ_p)+P}
=σ_p・(1－v²)－v・(1+v)・P
よって
σ_p=σ₀+{v・(1+v)}/(1－v²)・P
  =σ₀+{v/(1－v)}・P
ここで、ポアソン比:v=0.5であるので、σ_p=σ₀+P　となります。

この得られた最後の式が自封性(Automatic sealing)を示したものです。Ｏリングの場合は計算が少し難しくなりますが、同様な結果となります。

 

運動用シールの密封理論

弾性流体潤滑理論(Elastohydrodynamic lubrication =EHD潤滑）が現在の基本となっています。ここではその内容は、専門書に譲りまして、その導き方と油膜の厚さを考慮した考え方で進めていきます。
油膜の厚さは逆EHD潤滑により、計算できます。

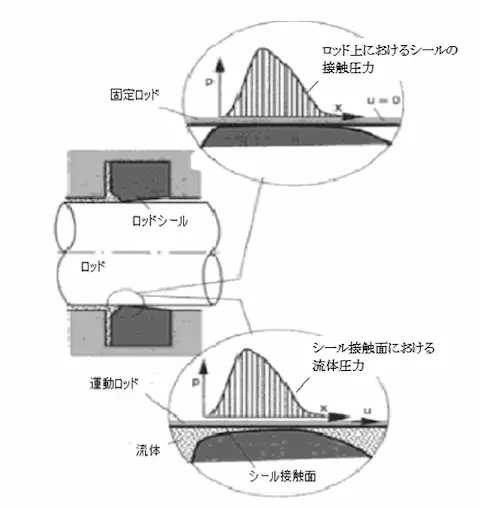
図3.1 ロッドシールの接触圧力分布

 

図では今迄に述べてきましたシールによる接触圧力が発生することはお分かりですが、逆にそのロッドとシール間の油膜の存在があります。（接触圧力とか接触応力とか混同していますが、同じ事象を言っています。シールから相手面に圧力を与えるが、逆にシールの内部では応力を受けることとなるためです。ここで、油膜にもシールがロッドを押している状態ですので、ロッドに掛かる接触圧力と同じ形態で油膜にも圧力が加わると考えます。（図3.1の下側に書いています流体圧力分布図に相当します。）

h：油膜厚さ
h₀：最大応力のかかっている油膜厚さ
η：油の粘性係数
u₀：ロッドの摺動速度

dpdx
：油膜にかかる圧力勾配

h³・d²pdx²+dhdx・(3h²dpdx－6ημ₀)=0 (2)

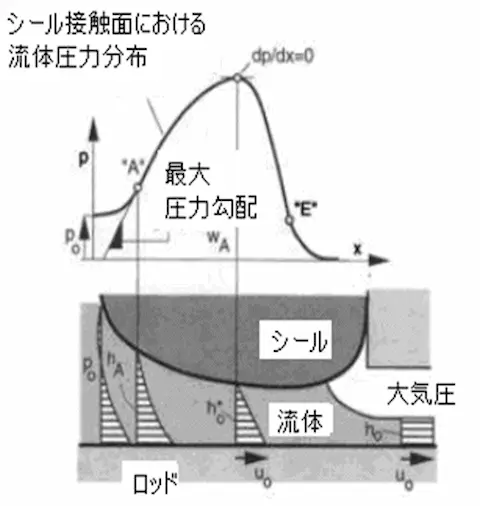
図3.2押し行程での流体圧力及び速度
分布（流体とは油膜のことです）

 

押し行程とはロッドが外部へ出ていくことを言います。戻り行程は逆にロッドがシリンダ内部に戻ることを言います。
(1)式を微分しますと(2)式になります。

h³・d²pdx²+dhdx・(3h²dpdx－6ημ₀)=0 (2)

 
 

図3.2でAの変曲点での油膜厚さh_Aは直接計算できます。

d²pdx² = 0 (A点にて)
　従って

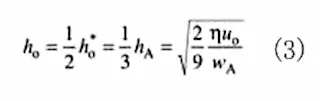
次に、A点でdhdx≠0であるので、[　 ]内が0となるので、W_A=dpdx_A とすると
A点の油膜厚さは

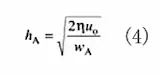
となります。押し行程での油膜厚さは、(1)式にこれらの結果を代入すると最大圧力の点におけるh₀*は次式となります。

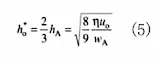
図3.2でdpdx=0の点で、u₀は0となる。
大気圧側では、油膜厚さはh₀ はh₀*の半分となります。

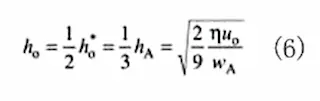
すなわち、押し行程ではこのh₀の油膜が出ていくことになります。

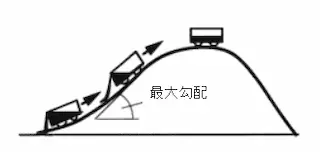
図3.4　最大勾配の漏れとの対比

 

図ではトロッコ一杯に入っている流体は勾配が大きいと多くの流体が漏れ出すことを例えています。勾配を大きくすることが出ていく油膜厚さが薄くなると言えます。

他方のロッドの引き行程でも同様な計算ができます。

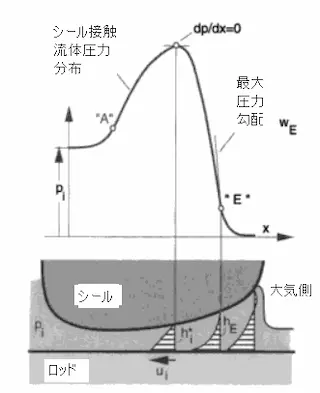
図3.5　引き行程における速度と油膜圧力分布

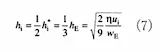
(7)式においては

hi： 引き行程の油膜厚さ

η：油の粘性係数

u_i：ロッドの速度

W_E：(dp/dx)圧力勾配

です。

 
 

従って、漏れは押し行程で出た油膜厚さが引き行程で戻される油膜厚さの差が漏れとなります。 次式に漏れの例を示します。(8)式

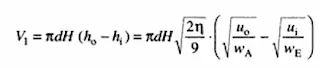
ここで

V₁:一行程における漏れ量

d：ロッド径

H：ストローク長さ

その他の文字の意味は先に述べています。
従って、シールの漏れを少なくする手段は、最終的にはシールの接触圧力に大きく依存していることになります。
まず、圧力側では接触圧力の立ち上がりの勾配が最大になるようなシールが必要となります（W_Aが大きいこと）。
また同様にこのシールの空気圧側での接触圧力勾配が最小になるようなシールが必要となります(W_Eが小さいこと)。このような設計を行なえば漏れを少なくできることになります。

 

以上のようなことを見ていきますとロッド用シールは完全に非対称形のシールでなければならないことが解ります。（例としては典型的なものはＵパッキンとなります。また特殊な組合せシールなどがあります）
なぜかと言いますと対称形のものは先ほど述べました接触圧力がシールの形に近い対称形になるのでW_AとW_Eに大きな差がでないためです。

 

文献では二つのシールで実例を挙げて比較しています。
図3.6がその接触応力を示しています。
Ｏリングは硬さ90でNBR です。（太さ（線径）は2.6mm）
組合せシールはステップシールKタイプで、35％ブロンズ入りのPTFE。

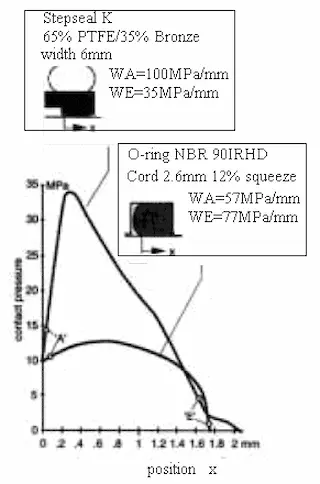
図3.6　10MPa時におけるＯリングと組合せシール（Stepseal K）の圧力分布

 

図のように間違いなく接触圧力の波形が違います。特に図に記載されていますようにW_AとW_Eには違いが見えます。 次に計算式を元に漏れに関して対比した場合の比較を説明します。

 

油膜厚さの対比の結果を表1に示します。

表１ 油膜厚さ（単位:nm）

シールの種類	ho 押し行程	hi 引き行程
Oリング	443	132
組合せシール(ステップシール)	91	211

試験の条件は次のとおりです。

• 1) 接触幅：約2mm
• 2) 速度：u₀ =u_i = 0.2m/s
• 3) 粘性係数(η) =0.03Pas

漏れの計算式は次のようになります。
V=NπDH (h₀－h_i)
それぞれ

• 1) V：漏れ量
• 2) π: 円周率
• 3) D：ロッド径 = 50mm
• 4) H：ストローク＝300mm
• 5) N：サイクル数=100サイクル

以上で表１と計算した結果は表２となります。

表２ 漏れ量の比較

シールの種類	漏れ量（ml）
Oリング	15
組合せシール(ステップシール)	0

これらのように理論から導き出した計算式により、実際の漏れが計算できる仕組みを説明しました。
重要なのは、シールの接触応力を導き出すことが一つのポイントとなります。
前に紹介しましたFEMがこのためにも役立つことがお分かりになったと思います。
シールの形状や材料も漏れを軽減できる要素を含んでいることも言うまでもありません。
密封理論は確かに、従来から多くの研究者が検討してきて歴史があります。
最近、ここまでにたどり着いた感がします。

 

その他にも多くの要素があることも事実であり、不確定要素も多くあります。
それらの不確定要素には

• 1) 環境温度の影響
• 2) 油温の影響
  （以上は油の粘性係数で見ているけれど）
• 3) ロッドの表面粗さ・負荷曲線
• 4) ロッドの金属材料・硬さ
• 5) シール表面の粗さ　など

このような要素については密封理論には含まれていません。

いままで、難しい理論の展開で、しかも説明が不十分なために理解し難いことがあったと思われます。
シールの摺動抵抗についても最近分かってきたことがありますが、ある式に入れればOKとはまだ言えない状況です。
シールの寿命も同様に推定できないため、あるモデルで実際に試験する以外の方法しかありません。それらはいずれも決定づける要素が多いためであるためです。これで密封理論は終わりにします。